Why is cos theta used in the formula of work?

Work : When a force acts for some time on a body, the product of the magnitude of the force and the displacement of its point of application in the direction of the force is defined to be the work done by the force.

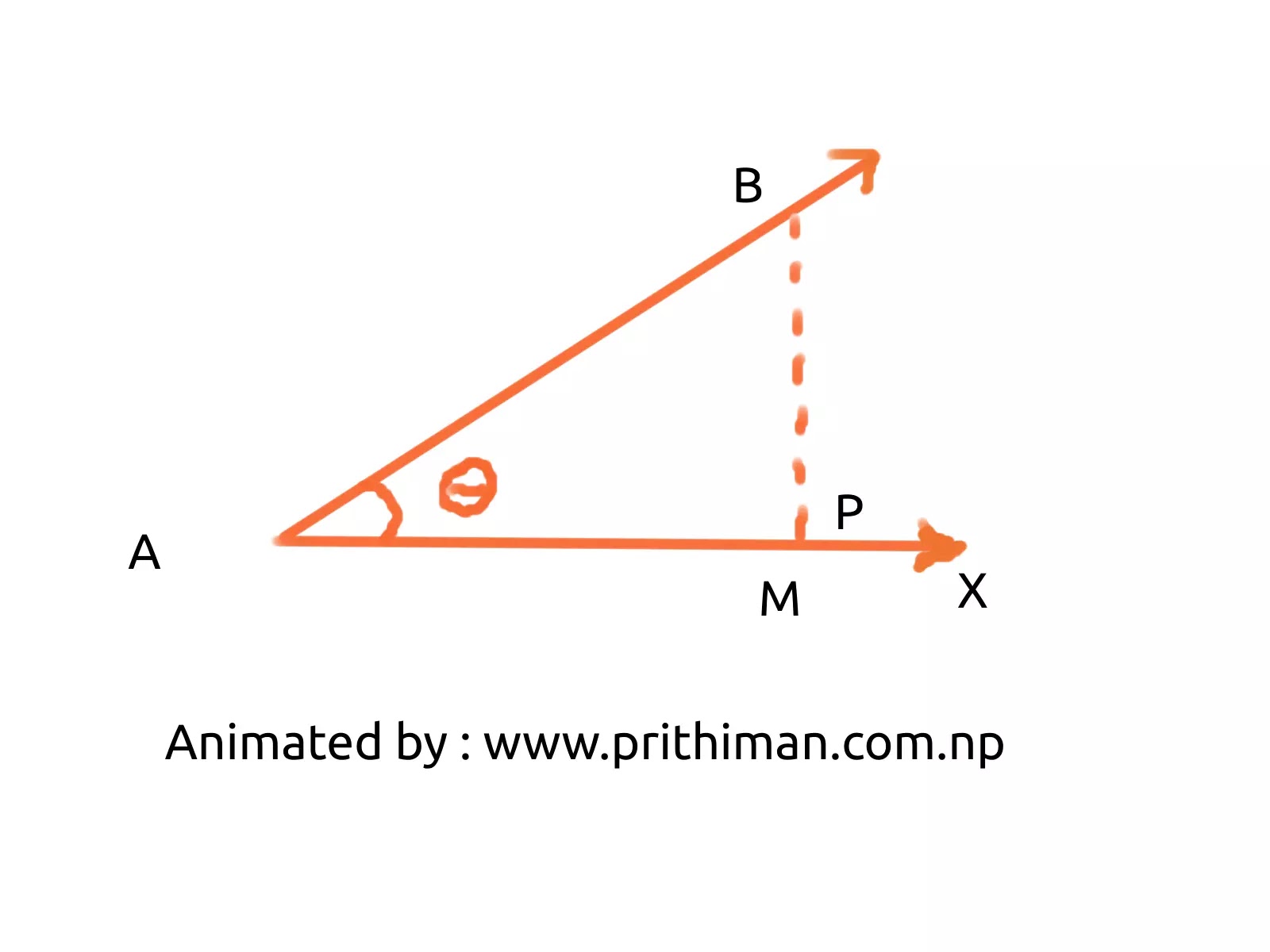
Suppose that a force P acts for some time on a body at the point A in the direction AX(above figure). If the point A moves to the position B under the action of the force, then AB measures the displacement of the point of application. Drop the perpendicular BM from B on AX. The displacement of the point of application in the direction of the force is then AM= ABcos(theta), where (theta) is the angle between the direction of the applied force and the displacement. Therefore , the work done by the force P is W=P.ABcos(theta) = AB.Pcos(theta) = force x component of the displacement of the point of application in the direction of the force = displacement of the point of application x component of the force along the displacement. work is a scalar quantity although the force and the displacement are both vector quantities. if (theta) is an acute angle, the component of the displacement along the force and the work done by the force, i.e. W , are positive . In this case, the applied force indeed does the work. If theta = 0, i.e. if the displacement occurs exactly in the direction of the force , the work done by the force attains its maximum value. On the other hand if theta is an obtuse angle , the component of the displacement in the direction of the force and the work done by the force, i.e. W , become negative. Here , work is actually done against the force. When theta = 180 , i.e. the point of application is displaced exactly opposite to the direction of the force, the work done against the force is a maximum.

A short Biography of famous scientist Galileo Galilei